无限长梯形网络等效电阻的求解

题目

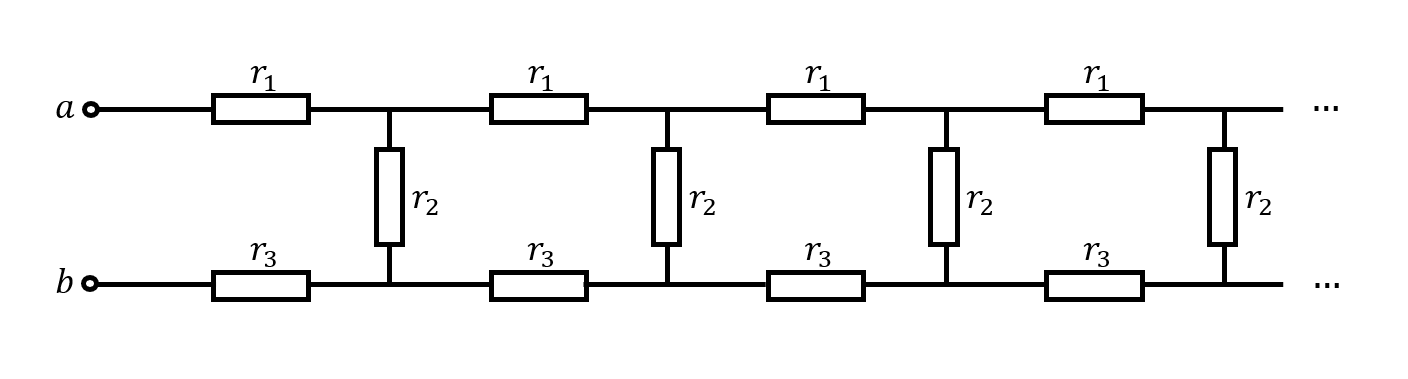
现有以电阻 $r_1=r_2=r_3=1\Omega$ 构成的一个无限长梯形网络（如图所示），求 $a,b$ 之间的等效电阻.

常规解法

将 $R_{ab}$ 去掉一个循环节的网络看作 $R_{ab}’$ ，如下图所示.

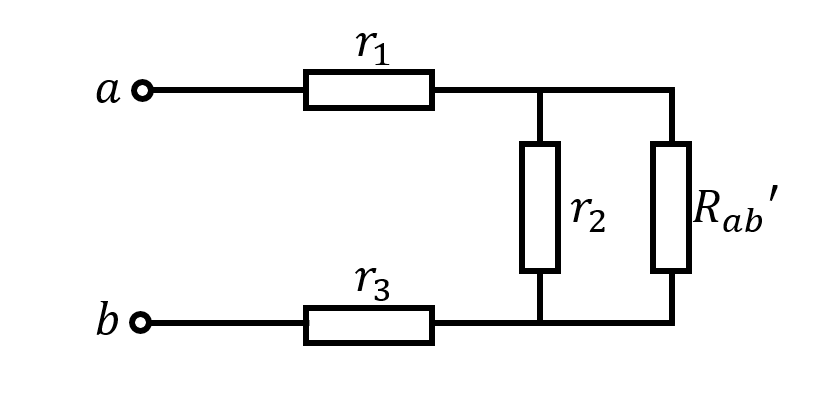
根据电阻串并联的规律知 $R_{ab}=r_1+\frac{r_2R_{ab}’}{r_2+R_{ab}’}+r_3$ .

由于有无穷多节，相差一节对电阻的影响微乎其微（可看作是无穷小），因此 $R_{ab}’=R_{ab}$ .

将 $r_1=r_2=r_3=1\Omega$ 代入后求得 $R_{ab}=1+\sqrt3\ \Omega$ .

常规解法的缺陷

常规解法虽然有一定道理，但使用“微乎其微”等形容词来描述不具有很强的说服力。另外，常规解法不能解决有限节梯形网络的问题，如果我们要求解的等效电阻并不是无穷多节的循环，而是有限节 $n$ 时的等效电阻，那么就不能使用常规解法来解决.

新型解法

我们不妨设这个梯形网络的节数为 $n$ ，此时 $a,b$ 之间的等效电阻为 $R_{ab}|_{n}$ ，观察下列情况

• 当 $n=1$ 时，$R_{ab}|_{n=1}=r_1+r_2+r_3$

• 当 $n=2$ 时，$R_{ab}|_{n=2}=r_1+\frac{r_2R_{ab}|_{n=1}}{r_2+R_{ab}|_{n=1}}+r_3$

• 当 $n=3$ 时，$R_{ab}|_{n=3}=r_1+\frac{r_2R_{ab}|_{n=2}}{r_2+R_{ab}|_{n=2}}+r_3$

• ……

• 当 $n=n$ 时，$R_{ab}|_{n}=r_1+\frac{r_2R_{ab}|_{n-1}}{r_2+R_{ab}|_{n-1}}+r_3$

由此，我们发现了对于一般的 $n$ ，存在 $R_{ab}|_{n}$ 与 $R_{ab}|_{n-1}$ 之间的递推关系式.

为简化计算，我们将 $r_1=r_2=r_3=1\Omega$ 代入，获得 $R_{ab}|_{n}$ 与 $R_{ab}|_{n-1}$ 之间的常量递推关系，并写以数列形式.

设$a_n=R_{ab}|_{n}$ ，则$a_{n-1}=R_{ab}|_{n-1}$ ，有 $a_n=\frac{3a_{n-1}＋2}{a_{n-1}＋1}\ (n≥2)$ ，其中 $a_1=3$ .

令 $x=\frac{3x+2}{x+1}$ ，即 $x^2-2x-2=0$ ，此方程存在两根 $x_1=1-\sqrt3,\ x_2=1+\sqrt3$ .

由于 $x_1≠x_2$ ，有 $\frac{a_{n}-x_1}{a_{n}-x_2}=q\frac{a_{n-1}-x_1}{a_{n-1}-x_2}$ ，其中 $q=\frac{3-x_1}{3-x_2}$ .

根据等比数列通项公式，知 $\frac{a_{n}-x_1}{a_{n}-x_2}=(\frac{3-x_1}{3-x_2})^n=(2+\sqrt3)^{2n}$ .

化简后求得 $a_n=\frac{(2+\sqrt3)^{2n}(1+\sqrt3)-(1-\sqrt3)}{(2+\sqrt3)^{2n}-1}\ (n≥2)$ ，为 $a_n$ 的封闭表达式.

因此 $R_{ab}|_{n}=a_n\ (\Omega)$ ，取极限 $R_{ab}=\lim\limits_{x\rightarrow\infty}a_n\ (\Omega)$ 即为无穷多节梯形网络的等效电阻.

$\lim\limits_{x\rightarrow\infty}a_n=\lim\limits_{x\rightarrow\infty}\frac{(2+\sqrt3)^{2n}(1+\sqrt3)-(1-\sqrt3)}{(2+\sqrt3)^{2n}-1}=\lim\limits_{x\rightarrow\infty}\frac{1+\sqrt3-\frac{1-\sqrt3}{(2+\sqrt3)^{2n}}}{1-\frac{1}{(2+\sqrt3)^{2n}}}=1+\sqrt3$ .

所以，对于有无穷多节的等效电阻 $R_{ab}=1+\sqrt3\ \Omega$ .

新型解法的优缺点

优点：对无限长梯形网络等效电阻问题给出了严谨的证明，且适用于一般有限节的情况.

缺点：过程较为复杂，求解难度大.